Without Calculating the Weighted Mean for the Combined Group

Photo by Marcin Jozwiak on Unsplash

Using Weighted M-Ways Clustering to Determine Distribution Centres Locations

Another utilize case of a modified version of K-means algorithm you might not know

Groundwork

All of usa must exist familiar with fast-food chain companies such as KFC or McDonalds, due to their massive number of outlets surrounding the states. Such names are well known for offer ready-to-eat meals speedily, thanks to advance-bulk cooking and sometimes besides pre-packaging. As an implication of their business model, fast-nutrient bondage require fast supply chain execution, peculiarly for the ingredients. This is to ensure they are e'er fresh to be served to the customers.

Regarding this, have yous ever been thinking about how they could provide such perishable ingredients promptly? This turns out not a simple problem as it may sound, due to the vast magnitude of the number of outlets involved. In this respect, distribution centers portrayed by warehouses take a critical role.

Fast-food bondage' warehouses are the place where the suppliers drib off their goods, which after packaged, and finally distributed to the outlets. Typically, a warehouse takes intendance of all outlets within a couple of cities around it. Because of this, fast-food chains would have several warehouses spread across their operating regions.

In this article, we consider a global fast-nutrient company that recently planned to enter the Indonesian market. The direction expects to execute this expansion in ii phases: Phase I and Phase II. The starting time stage will encompass only Java Island, while the rest regions will be handled on Stage 2. To this end, we volition help to determine its warehouses' locations, specifically for Stage I.

We will help a fast-nutrient restaurant to determine their warehouses' locations spreading beyond Java Island.

Recalling (Standard) K-Means Clustering

1000-means clustering is an algorithm for sectionalization the data into Thousand distinct clusters. The high-level view on how the algorithm works is as follows. Given a (typically random) initiation of One thousand clusters (which implied from Chiliad centroids), the algorithm iterates between two steps below:

1. Computing the distances between all data points and the existing G centroids and re-assigning each data point to its nearest centroid accordingly.
2. Calculating the new K centroids, by taking the information points' hateful, based on this new clustering assignment.

The above iteration is executed until the centroids do not change over iterations (algorithm converged) or a specific stopping criterion has been satisfied (e.thou., max number of iterations is triggered)

As the readers might have known, the number K in this algorithm is a hyperparameter (i.e., predefined number). In practice, we can select the optimal Thousand by using, for example, the Elbow method, which we volition use and explain later in the article.

Moreover, there is also a degree of freedom in picking the altitude metric, rather than the standard Euclidean distance used in the original algorithm. If necessary or seen more appropriate, nosotros can use other distance metrics such as Haversine altitude (the one nosotros will utilize in the article) or Manhattan distance.

Solving the problem using weighted K-means clustering

Let's go back to our problem! Determining the warehouses' locations tin can exist seen as finding centroids of clusters of the corresponding served branches. Therefore, this is an fantabulous use case of K-ways clustering, specifically weighted K-means clustering. What nosotros mean on 'weighted' will be credible in a moment.

We accept already known in the kickoff place that the fast-food company will open branches across Java. Nosotros can, therefore, address the trouble by first identifying the co-operative's locations, which nosotros can reasonably estimate with the longitude-latitude — comparable to (x,y) — of all cities/districts in Java. Using these data points of metropolis centers, we can actually run the standard Thousand-ways clustering to solve the trouble already. All the same, this approach would fail to have into account the fact that some cities are indeed bigger than others, which implies having a higher volume need for ingredients to exist supplied.

The standard M-means approach would neglect to take into account the fact that some cities are indeed bigger than others, which implies having a college volume demand for ingredients to be supplied.

In light of this, we too include population data for condign proxy to ingredient demands. These population information will and so be the weight of corresponding cities (information points) and voila! We have had the setting to run the weighted Thou-means clustering algorithm.

To give an interpretation of the influence of the weights on the algorithm, imagine nosotros are at present working with data points with different sizes (represented by their weights). We can further encounter the size to be proportional to the gravitational force owned by the information signal. Thus, the bigger the weight is, the stronger a data point pulls the centroid to be closer to it. In summary, the ultimate departure from the standard algorithm is on centroid calculation, where at present weighted averages are used, instead of standard means.

Illustration of standard (left) vs weighted (right) mean for calculating centroids

The information sources

We are grateful to this repository of benangmerah GitHub account for providing the data of longitude-latitude coordinates of the considered cities. It turns out that there are 119 cities in Java Island, from Cilegon in the due west to Banyuwangi in the left function shut to Bali. Moreover, we refer to BPS (Indonesian Bureau of Statistics) for the cities breakdown population data within each Java province in 2018.

Haversine Altitude

Note that we will be working with longitude-breadth, which represents the world's spherical surface — every bit opposed to the standard plain 2D coordinates system in (x,y). Because of this, the Euclidean distance is not the best distance metric to apply hither. Instead, nosotros will use the Haversine altitude, which is an appropriate altitude metric on a spherical surface.

The following equation where φ is latitude, λ is longitude, R is globe's radius (mean radius = 6,371km) is how we summate distance using the Haversine method (notate as d).

a = sin²(( φB — φA) /2) + cos φA * cos φB * sin²((λB — λA) /2)

c = 2 * atan2( √a, √(one−a) )

d = R ⋅ c

An R implementation of this altitude metric is given below.

          #haversine distance part          haversine_dist = function(point1, point2) { #each argument is a numeric vector with two elements (lon, lat)
            lon1 = point1[1]            
            lat1 = point1[2]
            lon2 = point2[1]
            lat2 = point2[2]
                R = 6371000 #earth radius in meters
              phi1 = lat1 * pi / 180 #convert to radian
              phi2 = lat2 * pi / 180 #convert to radian
              delta_phi = (lat2 - lat1) * pi / 180
              delta_lambda = (lon2 - lon1) * pi / 180
            
                a = (sin(delta_phi/2))^two + cos(phi1) * cos(phi2) * ((sin(delta_lambda/2))^2)
              c = ii * atan2(sqrt(a), sqrt(one-a))
            
                distance = R * c #haversine altitude between point1 and signal 2 in meters
              render(round(distance, 2))
}
                  

Step by footstep solution and codes in R

Ok, let's hands-on with the code! In this article, we volition use R to run the algorithm.

• Data preparation

We import a DataFrame that contains the required columns: city name, longitude, latitude, and population.

          df_city = read.csv('/Users/parara/Documents/Project/Weighted Chiliad-Means/city_data.csv')          head(df_city)        

head(df_city)

• Initialization

We fix the number of clusters K, say 5. Next, we randomly choose five cities to go the initial centroids. Afterward, using these centroids, we assign each city to its nearest centroid (initial cluster). Retrieve that we utilise Haversine distance every bit the distance metric.

          #number of clusters
K = five          #initial centroids by random
init_centroids_index = sample(nrow(df_city),Chiliad)          #initiate containers
distance_matrix = matrix(information = NA, nrow = nrow(df_city), ncol = One thousand)
cluster = vector()
centroid_long = vector()
centroid_lat = vector()          #compute distance betwixt cities and initial centroids
for (k in c(i:K)) {
            for (i in c(1:nrow(df_city))) {
            city_i = as.numeric(df_city[i,2:3])
            centroid_k = as.numeric(df_city[init_centroids_index[g],ii:3])
            distance_matrix[i,k] = haversine_dist(city_i,centroid_k)
            }
}          #initial cluster assignment for each city
for (i in c(i:nrow(df_city))) {
            cluster[i] = which.min(distance_matrix[i,])
}        

• The looping

Having the initial clusters, we are prepare to carry out the looping. We iteratively update centroids and re-assign cities to clusters, which nosotros do until cluster assignments are unchanged between iterations.

          #iteration baseline
old_cluster = vector(length = length(cluster))
new_cluster = cluster          #iterations
while (!all(old_cluster == new_cluster)) {
            #update old cluster assignment
            old_cluster = new_cluster
            #summate centroids using weighted average
            for (k in c(1:K)) {
            cluster_k = which(old_cluster == one thousand) #urban center index of cluster k
            centroid_long[grand] = weighted.mean(df_city$longitude[cluster_k], df_city$population[cluster_k])
            centroid_lat[k] = weighted.mean(df_city$breadth[cluster_k], df_city$population[cluster_k])
            }
            df_centroid = every bit.information.frame(cbind(centroid_long, centroid_lat))
            #compute distance between cities and centroids
            for (k in c(ane:K)) {
            for (i in c(1:nrow(df_city))) {
            city_i = as.numeric(df_city[i,two:3])
            centroid_k = equally.numeric(df_centroid[k,])
            distance_matrix[i,k] = haversine_dist(city_i,centroid_k)
            }
            }
            #update cluster assignment for each city
            for (i in c(one:nrow(df_city))) {
            cluster[i] = which.min(distance_matrix[i,])
            }
            #update new_cluster
            new_cluster = cluster
}        

• Choosing the best K

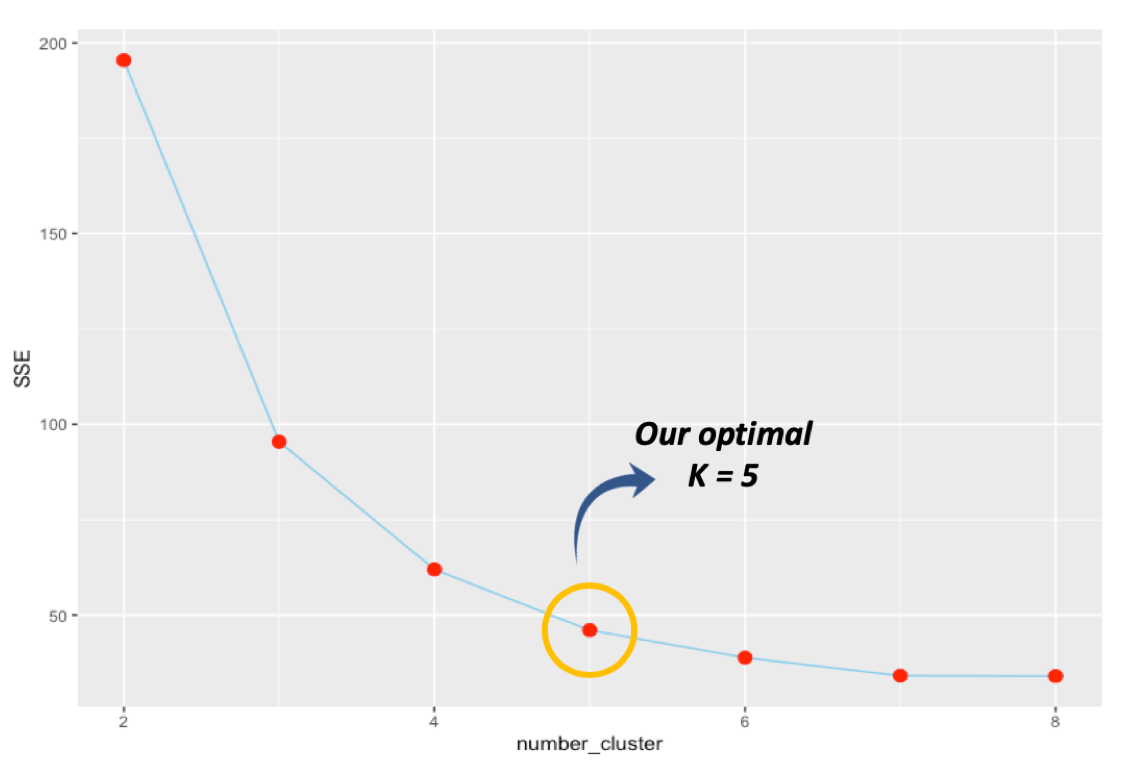
The truth is, the value of Chiliad = 5 selected in the above is made retrospectively. Nosotros had beforehand picked the number based on the following elbow method. But, understanding the technique requires usa first to comprehend what and then-called sum of squares mistake (SSE). In the K-means algorithm, the term "error" in SSE refers to the deviation betwixt a information point to its centroid. Therefore, we get the value of SSE by summing all of such squared errors for all data points.

We note that any clusters assignment corresponds to an SSE value. Thus, we tin can plot the SSE values of the converged algorithms at various Chiliad (number of clusters). Using this plot, we await at G at which the decline slopes subsequently the value are no longer pregnant. This is an optimal K we are looking for. Typically, this K value would course an 'elbow shape' on the overall plot hence the proper name.

For ours, the plot is given below. Note that the decline of SSE is no longer significant after K = 5 and hence we choice this number as the optimal K.

SSE declines over different Chiliad

• Result

Finally, the result of the algorithm is given below.

Weighted K-means result

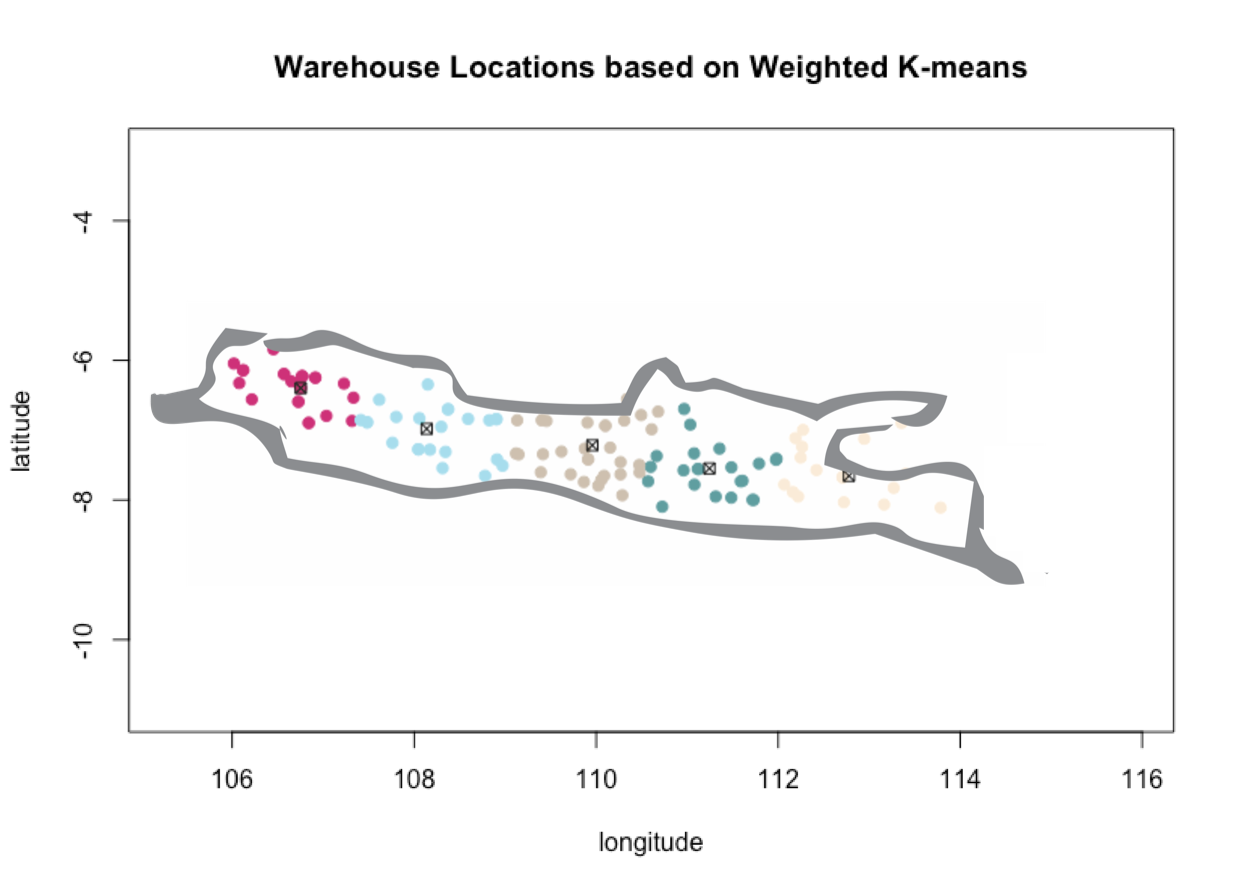
Based on the result above, our recommendation of 5 warehouses locations is thus as follows:

1. Near Depok, West Java
2. Near Majalengka, West Java
3. About Temanggung, Central Coffee
4. Near Madiun, East Java
5. Nearly Probolinggo, E Java

Conclusion and remark

In this article, we take demonstrated an application of the weighted Thousand-means clustering algorithm to decide warehouses' locations of a fast-nutrient eating place. To summarize, this modified version of K-means differs from the original one in the way it calculates the clusters' centroids, which uses the weighted average instead of the regular mean.

A final remark remains regarding our implementation (codes given in this postal service). K-means algorithm yields merely local optimum instead of the global one. That is, the final cluster consignment obtained depends on the initial assignment, which is random. Therefore, in the existent application, we need to replicate the whole algorithm several times and pick results from the all-time replication that yields the smallest SSE.

For interested readers, I put the code for this 'real implementation' in my GitHub repository here. There, you lot can also find the codes for SSE function, generating plots displayed in this post, and of class, the dataset used in this commodity.

All in all, thanks for reading and let's connect with me on LinkedIn at https://world wide web.linkedin.com/in/pararawendy-indarjo-5b87bab7.

syedcauz1949.blogspot.com

Source: https://towardsdatascience.com/using-weighted-k-means-clustering-to-determine-distribution-centres-locations-2567646fc31d

Share this post